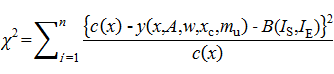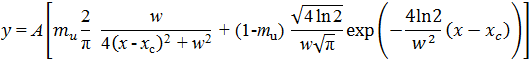
Active Shirley background subtraction algorithm is proposed by R. Matsumoto, Y. Nishizawa and H. Tanaka.
The main point in the active Shirley method is that the starting and ending points are regarded as fitting parameters, and the background is not forced to cross the spectrum at the starting and ending points. A spectrum, background of which is subtracted by non-iterative Shirley method, is deconvoluted to the pseudo-Voigt functions, and find the best matching parameters of functions. As the result of this process, the best matching background line is given. The pseudo- Voigt function used is given as follows.
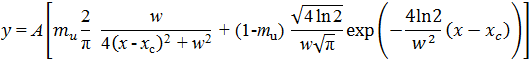
The first term in the above equation is Lorentzian and the second term is Gaussian. In this case, A is the peak height, w is the full width at half maximum (FWHM), xc is the peak position and mu is the mixing ratio of the Lorentzian. By changing the value of mu, we can freely produce a more practical function that has both Lorentzian and Gaussian characteristics. The specific algorithm in the active Shirley method is shown by the following steps:
(1) Estimate a tentative background using the non-iterative Shirley method.
(2) Determine the candidate peaks and initial parameters for peak fitting process from an original spectrum after elimination of the tentative background. The peak position and FWHM of the peak are obtained from the third derivative curve of the original spectrum.
(3) Modify the parameters of the pseudo-Voigt functions and the non-interative Shirley background using the Marquardt-Levenberg algorithm to reduce the difference between the experimental spectrum from XPS and the spectrum composed of the pseudo-Voigt functions and the background.
(4) The fitting parameters are then optimized to minimize kai-square value as shown below.